tg-me.com/knowledge_accumulator/265
Last Update:
Gumbel-Softmax - памятка себе на будущее
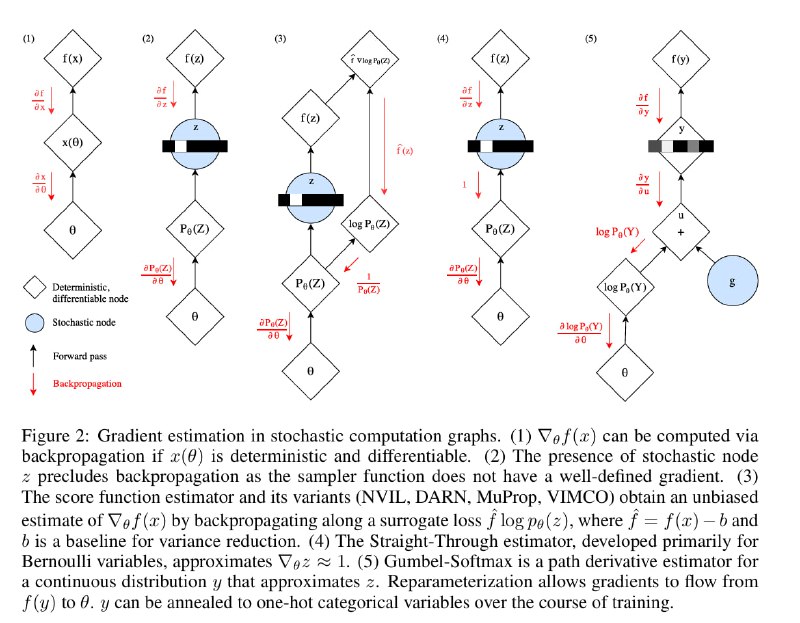
Итак, представим что у нас есть какая-то вероятностная модель, в которой сэмплирование из распределения является её частью. Самым банальным примером, пожалуй, является VAE.
VAE - это автоэнкодер, состоящий из моделей q(z|x) и p(x|z), которые выдают распределение на скрытую компоненту z по входу x и наоборот. В базовом варианте z имеет нормальное распределение N(m;d), и энкодер выдаёт параметры этого распределения - средние m и ст. отклонения d.
При обучении подобной модели у нас возникает градиент ошибки по сэмплу из z. Как пробросить градиент назад в модели "сквозь" это сэмплирование? В лоб сделать это не получится, и для этого применяют простой советский Reparametrization Trick.
Его суть в том, что процесс сэмплирования отделяют от основной цепочки вычислений и оформляют как входную вершину вычислительного графа. В случае с нормальным распределением, мы сначала отдельно сэмплируем eps из N(0;1), а затем умножаем его на d и прибавляем m. По факту результат тот же самый, но он превращает нейросеть в цепочку детерминированных операций и позволяет пробрасывать градиент бэкпропом.
Gumbel-Softmax - то же самое, но для категориального распределения.
Вместо обычного VAE давайте взглянем на VQ-VAE - альтернативный вариант автоэнкодера, в котором вместо сжатия в нормальное распределение происходит сжатие в категориальное распределение на "коды". Внутри модели хранится Codebook, который превращает номер кода обратно в эмбеддинг во время декодинга.
Итак, в сердцевине модели находится такая цепочка вычислений: logits -> probs -> one-hot vector -> embedding. При переходе из probs к one-hot vector как раз и возникает сэмплирование из категориального распределения, сквозь которое нельзя пробросить градиент напрямую.
Gumbel-Softmax позволит приближенно осуществить этот переход с помощью детерминированной операции. Если к логарифму от вектора probs прибавить вектор из распределения Гумбеля (аналог N(0;1) в данном случае), то argmax итогового вектора будет распределён так же, как и исходное распределение.
Последняя проблема - argmax сам недифференцируем, поэтому его заменяют на софтмакс с маленькой температурой. В итоге, получая на вход [0.2;0.8], эта операция будет выдавать [0.001; 0.999] в 80% случаев и [0.999;0.001] в 20 процентах случаев.
Самый большой затык вызывает следующий вопрос - в чём профит этой штуки по сравнению с тем, чтобы просто использовать [0.2;0.8] в дальнейших операциях, если там всё равно не требуется строгий one-hot вектор?
Я объясняю это так - во время обучения мы хотим, чтобы все последующие части модели получали на вход реалистичные сэмплы из категориального распределения. Если наша модель будет учиться на размазанных векторах, то мы не сможем во время инференса просто начать сэмплировать код - декодер не выкупит этот пранк.
А что делать в случае, когда нам реально нужен строгий one-hot вектор, например, если это RL и мы совершаем действие? Авторы оригинальной статьи предлагают комбинировать Straight Through Estimator и Gumbel Softmax, т.е. использовать [1; 0], а градиент пробрасывать так, как будто там был [0.999; 0.001]. Но я никогда не встречал применения такой схемы.
@knowledge_accumulator
BY Knowledge Accumulator
Share with your friend now:
tg-me.com/knowledge_accumulator/265
